PSU_STAT505_MVA

STAT505 Hierarchical Cluster

Ramaa Nathan 4/20/2019

This is a R impelmentation of the hierarchical clustering example used in the on-line notes of STAT 505. This example uses ecological data from Woodyard Hammock, a beech-magnolia forest in northern Florida. The data involve counts of the numbers of trees of each species in n = 72 sites. A total of 31 species were identified and counted, however, only p = 13 of the most common species were retained and are listed below. They are:

Species Code Latin Name Common Name
carcar Carpinus caroliniana Ironwood
corflo Cornus florida Dogwood
faggra Fagus grandifolia Beech
ileopa Ilex opaca Holly
liqsty Liquidambar styraciflua Sweetgum
maggra Magnolia grandiflora Magnolia
nyssyl Nyssa sylvatica Blackgum
ostvir Ostrya virginiana Blue Beech
oxyarb Oxydendrum arboreum Sourwood
pingla Pinus glabra Spruce Pine
quenig Quercus nigra Water Oak
quemic Quercus michauxii Swamp Chestnut Oak
symtin Symplocus tinctoria Horse Sugar

The objctive of this data is to group sample sites together into clusters that share similar species compositions as determined by some measure of association. In this document, we will be using agglomerative heracrchical clustering techniques.

Data Exploration

Load File

wood = read_table("data/wood.txt", col_names=c("x", "y","acerub","carcar","carcor","cargla","cercan","corflo","faggra","frapen",
  "ileopa", "liqsty","lirtul","maggra","magvir","morrub","nyssyl","osmame","ostvir","oxyarb","pingla","pintae","pruser", "quealb","quehem","quenig",
  "quemic","queshu","quevir","symtin","ulmala","araspi","cyrrac") )

## Parsed with column specification:
## cols(
##   .default = col_integer()
## )

## See spec(...) for full column specifications.

#Dimensions of the table read in
dim(wood)

## [1] 72 33

#We are only interested in 13 species (here they will be considered as 13 variables)
excluded_vars <- c("acerub","carcor","cargla","cercan","frapen","lirtul","magvir","morrub","osmame","pintae","pruser",
                   "quealb","quehem","queshu","quevir","ulmala","araspi","cyrrac")

#Filter out the variables
wood <- wood %>% 
  mutate(ident = row_number()) %>%
  select (-one_of(excluded_vars))

#Check the dimensions and column names of the final dataframe
dim(wood)

## [1] 72 16

colnames(wood)

##  [1] "x"      "y"      "carcar" "corflo" "faggra" "ileopa" "liqsty"
##  [8] "maggra" "nyssyl" "ostvir" "oxyarb" "pingla" "quenig" "quemic"
## [15] "symtin" "ident"

Hierarchical Clustering

Complete Linkage

We will use the Euclidean distance as the dissimilarity measure. In R, the dist() fucntion computes the Euclidean distance between the rows of the matrix. In our example, we only want to compute the distances for the 13 variables. So, we will use wood\[,3:15\]

# we only want to use the columns 3 throught 15 for computing the disimilarities
hc_complete <- hclust(dist(wood[,3:15]),method="complete")

#extract the dendrogram 
hc_complete_den <- as.dendrogram(hc_complete)

# use ggdendrogram (basaed on ggplot2) to plot the dendrograms
ggdendrogram(hc_complete,size=2,rotate=TRUE,scale=2) +
  labs(title="Dendrogram - Complete Linkage") +
  xlab("Height") + ylab("Sites")

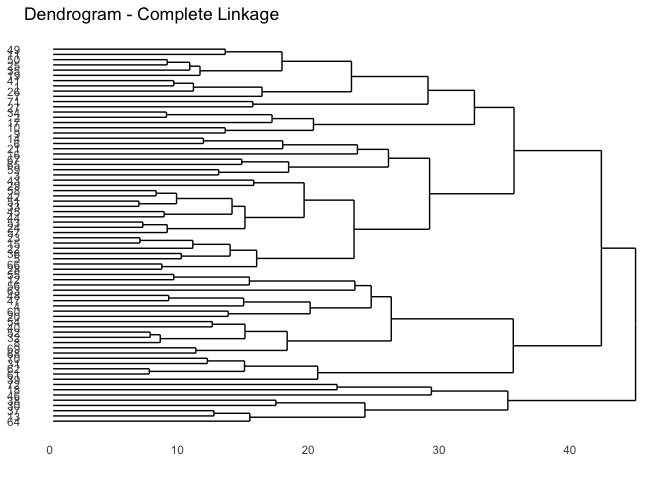
We want to next find the history of the different merges in forming the different clusters. From the documentation, the order of merges is as follows: Row i of merge describes the merging of clusters at step i of the clustering. If an element j in the row is negative, then observation -j was merged at this stage. If j is positive then the merge was with the cluster formed at the (earlier) stage j of the algorithm. Thus negative entries in merge indicate agglomerations of singletons, and positive entries indicate agglomerations of non-singletons. The Max distance is the maximum distance computed between the two clusters as required for complete linkage

hc_complete_hist <- as_data_frame(cbind(hc_complete$merge,hc_complete$height))
colnames(hc_complete_hist)<- c("ClusterA","ClusterB","Max Distance")
hc_complete_hist <- hc_complete_hist %>%
  mutate ("Merge Order" = row_number()) %>% 
  select(`Merge Order`, ClusterA, ClusterB, `Max Distance`)
formatAsTable(hc_complete_hist,"Clustering History")
Clustering History
Merge Order ClusterA ClusterB Max Distance
1 -33 -51 6.557438
2 -15 -23 6.633250
3 -24 -53 6.855655
4 -61 -62 7.348469
5 -32 -52 7.416199
6 -42 -58 7.874008
7 -8 5 8.185353
8 -28 -66 8.306624
9 -44 -45 8.485281
10 -2 -34 8.660254
11 -57 3 8.717798
12 -25 -50 8.717798
13 -47 -48 8.831761
14 -1 -41 9.219544
15 -12 -55 9.219544
16 1 6 9.433981
17 -5 -36 9.797959
18 -35 12 10.440307
19 -22 2 10.677078
20 -26 14 10.723805
21 -68 -69 10.908712
22 -19 18 11.224972
23 -6 -14 11.489125
24 -31 -70 11.789826
25 -40 -54 12.165525
26 -13 -37 12.288206
27 -3 -59 12.649111
28 -9 -10 13.152946
29 -11 -49 13.152946
30 -20 -60 13.379088
31 17 19 13.527749
32 9 16 13.674794
33 -65 -67 14.422205
34 -4 13 14.560220
35 4 24 14.628739
36 7 25 14.662878
37 11 32 14.662878
38 -56 15 15.000000
39 -64 26 15.033296
40 -27 -71 15.264337
41 -29 -43 15.329710
42 8 31 15.556349
43 -7 20 15.968719
44 -17 10 16.733200
45 -30 -38 17.029386
46 22 29 17.492856
47 -21 23 17.549929
48 21 36 17.888544
49 27 33 18.000000
50 37 41 19.183326
51 30 34 19.646883
52 28 44 19.899749
53 -39 35 20.223748
54 -18 -72 21.702534
55 43 46 22.803508
56 42 50 23.000000
57 -63 38 23.065125
58 -16 47 23.259407
59 39 45 23.832751
60 51 57 24.310492
61 49 58 25.632011
62 48 60 25.845696
63 40 55 28.653098
64 56 61 28.774989
65 -46 54 28.913665
66 52 63 32.202484
67 59 65 34.756294
68 53 62 35.171011
69 64 66 35.227830
70 68 69 41.904654
71 67 70 44.519659

Cluster numbers

hc_complete_clusters = as_data_frame(cbind(wood$ident,cutree(hc_complete, k=6)))
colnames(hc_complete_clusters) <- c("Identity","Cluster")
formatAsTable(hc_complete_clusters,"Clusters")
Clusters
Identity Cluster
1 1
2 1
3 2
4 3
5 2
6 2
7 1
8 3
9 1
10 1
11 1
12 3
13 4
14 2
15 2
16 2
17 1
18 5
19 1
20 3
21 2
22 2
23 2
24 2
25 1
26 1
27 1
28 2
29 2
30 4
31 6
32 3
33 2
34 1
35 1
36 2
37 4
38 4
39 6
40 3
41 1
42 2
43 2
44 2
45 2
46 5
47 3
48 3
49 1
50 1
51 2
52 3
53 2
54 3
55 3
56 3
57 2
58 2
59 2
60 3
61 6
62 6
63 3
64 4
65 2
66 2
67 2
68 3
69 3
70 6
71 1
72 5

Interpret the Clusters by doing an ANOVA on all the variables

wood_cluster <- wood %>% mutate(cluster = cutree(hc_complete,k=6))

# WE could do an ANOVA fit with one model statement - but it is difficult to extract the individual p-values.
manova_fit <- manova(cbind(carcar, corflo, faggra, ileopa, liqsty, maggra, nyssyl, ostvir, oxyarb, 
     pingla,quenig, quemic, symtin) ~ factor(cluster), data=wood_cluster)
str(summary.aov(manova_fit))

## List of 13
##  $  Response carcar:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 4341 910
##   ..$ Mean Sq: num [1:2] 868.2 13.8
##   ..$ F value: num [1:2] 62.9 NA
##   ..$ Pr(>F) : num [1:2] 8.81e-24 NA
##  $  Response corflo:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 32.7 278.6
##   ..$ Mean Sq: num [1:2] 6.54 4.22
##   ..$ F value: num [1:2] 1.55 NA
##   ..$ Pr(>F) : num [1:2] 0.187 NA
##  $  Response faggra:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 538 999
##   ..$ Mean Sq: num [1:2] 107.6 15.1
##   ..$ F value: num [1:2] 7.11 NA
##   ..$ Pr(>F) : num [1:2] 2.27e-05 NA
##  $  Response ileopa:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 480 1850
##   ..$ Mean Sq: num [1:2] 96 28
##   ..$ F value: num [1:2] 3.42 NA
##   ..$ Pr(>F) : num [1:2] 0.00824 NA
##  $  Response liqsty:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 833 1875
##   ..$ Mean Sq: num [1:2] 166.7 28.4
##   ..$ F value: num [1:2] 5.87 NA
##   ..$ Pr(>F) : num [1:2] 0.000152 NA
##  $  Response maggra:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 111 370
##   ..$ Mean Sq: num [1:2] 22.3 5.6
##   ..$ F value: num [1:2] 3.97 NA
##   ..$ Pr(>F) : num [1:2] 0.00329 NA
##  $  Response nyssyl:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 36.7 292.1
##   ..$ Mean Sq: num [1:2] 7.35 4.43
##   ..$ F value: num [1:2] 1.66 NA
##   ..$ Pr(>F) : num [1:2] 0.157 NA
##  $  Response ostvir:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 1531 1141
##   ..$ Mean Sq: num [1:2] 306.1 17.3
##   ..$ F value: num [1:2] 17.7 NA
##   ..$ Pr(>F) : num [1:2] 4.35e-11 NA
##  $  Response oxyarb:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 34.4 320.2
##   ..$ Mean Sq: num [1:2] 6.88 4.85
##   ..$ F value: num [1:2] 1.42 NA
##   ..$ Pr(>F) : num [1:2] 0.229 NA
##  $  Response pingla:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 39.6 1209.9
##   ..$ Mean Sq: num [1:2] 7.93 18.33
##   ..$ F value: num [1:2] 0.432 NA
##   ..$ Pr(>F) : num [1:2] 0.824 NA
##  $  Response quenig:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 65 384
##   ..$ Mean Sq: num [1:2] 13.01 5.83
##   ..$ F value: num [1:2] 2.23 NA
##   ..$ Pr(>F) : num [1:2] 0.0612 NA
##  $  Response quemic:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 304 974
##   ..$ Mean Sq: num [1:2] 60.8 14.8
##   ..$ F value: num [1:2] 4.12 NA
##   ..$ Pr(>F) : num [1:2] 0.00256 NA
##  $  Response symtin:Classes 'anova' and 'data.frame':    2 obs. of  5 variables:
##   ..$ Df     : num [1:2] 5 66
##   ..$ Sum Sq : num [1:2] 2252 393
##   ..$ Mean Sq: num [1:2] 450.32 5.96
##   ..$ F value: num [1:2] 75.6 NA
##   ..$ Pr(>F) : num [1:2] 5.79e-26 NA
##  - attr(*, "class")= chr [1:2] "summary.aov" "listof"

# So, do a separate anova for each response variable and create a list of the fits
fitlist = sapply(wood_cluster[,3:15],function(resp) summary(aov(resp ~ factor(cluster), data=wood_cluster)))
response_names <- names(fitlist)
str(fitlist[[1]]["Pr(>F)"])

## Classes 'anova' and 'data.frame':    2 obs. of  1 variable:
##  $ Pr(>F): num  8.81e-24 NA

sig_responses = NULL
for(l in seq_along(fitlist)) {
  #print(fitlist[l])
  if(fitlist[[l]]$"Pr(>F)"[1] < (0.05/13)) {
    print(paste(response_names[l],": ",fitlist[[l]]$"Pr(>F)"[1]))
    sig_responses = append(sig_responses,response_names[l])
  }
}

## [1] "carcar :  8.80852922183047e-24"
## [1] "faggra :  2.27190383668137e-05"
## [1] "liqsty :  0.000152444655166322"
## [1] "maggra :  0.00328752181365586"
## [1] "ostvir :  4.35436167576968e-11"
## [1] "quemic :  0.0025566026778279"
## [1] "symtin :  5.79053974855473e-26"

#sig_responses
paste("Significant Variables:")

## [1] "Significant Variables:"

sig_responses

## [1] "carcar" "faggra" "liqsty" "maggra" "ostvir" "quemic" "symtin"

Get the cluster means of only the significant response variables

cluster_means <- wood_cluster %>% group_by(cluster) %>% summarise_at(vars(sig_responses),mean)
formatAsTable(cluster_means,"Cluster Means of Significant Variables")
Cluster Means of Significant Variables
cluster carcar faggra liqsty maggra ostvir quemic symtin
1 1.235294 5.941177 6.764706 3.2352941 13.823529 4.117647 2.0000000
2 3.846154 11.384615 7.192308 5.2692308 4.269231 5.269231 0.9230769
3 18.500000 5.937500 6.437500 2.7500000 2.875000 9.375000 0.6875000
4 8.200000 8.600000 6.600000 4.6000000 3.600000 7.000000 18.0000000
5 6.000000 2.666667 18.000000 0.6666667 14.000000 2.333333 20.0000000
6 24.400000 6.400000 17.400000 3.8000000 2.800000 5.200000 0.0000000